Capital market line

Я давеча открыл для себя Capital market line (CML).

Можно было бы об этом не делать пост, ведь есть статья в вики. Но статья там херовая. У формулы нет описания переменных. Даже в английской версии статьи. Позор какой-то. Поэтому я решил пографоманить, а заодно записать еще свои выводы из всего этого.

Итак, если собрать портфель из нескольких инструментов, то можно выбрать им разные веса. Если перебрать все возможные варианты комбинаций разных весов, то получится что-то типа такого:

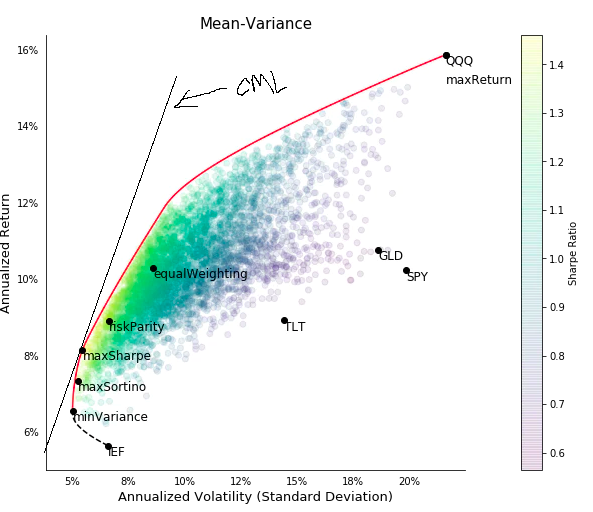Картинка сперта отсюда.

Каждое сине-зелено-желтое пятно соответствует портфелю. По вертикале - доходность. По горизонтале - риск. Красная линия - так называемая линия фронта эффективного портфеля. Все, что ниже этой линии - херовый портфель, т.к. при той же величине риска можно получить большую доходность, если получше выбрать веса инструментам.

Линия CML проходит через две точки:

1) точку нулевого риска и безрисковой ставки. Но это в теории. На практике надо брать ставку под которую можно делать займ у своего брокера.

2) точку портфеля, у которого максимальный коэфициент Шарпа. И это точка оказывается всегда является точкой касания линии фронта! Почему так - будет понятно позже.

А теперь главное: только точка с максимальным коэфициентом Шарпа является оптимальной. Все остальные точки кривой “эффективного” фронта херовые. Их не стоит выбирать!

Для точек кривой фронта с риском меньше чем в точке maxSharp лучше добавить безрисковый актив, т.е. взять облигаций в портфель. Так можно при том же уровне риска получить большую доходность.

Для точек кривой фронта с риском больше чем в точке maxSharp, лучше выбрать точку с максимальным коэфициентом Шарпа и воспользоваться рычагом, т.е. занять денег у брокера. Тогда можно будет получить прибыль больше при том же уровне риска.

Почему так? Какие ваши доказательства?

Формула для расчета дохода при использовании рычага: RL = R + (L - 1) * (R - Rf), где L - размер рычага, например, если занять столько же средств, сколько в портфеле, то L = 2. Rf - ставка по кредиту (“рефинансирование”).

Почему такая формула? Первое слагаемое R - это просто доходность исходного портфеля без рычага. Дальше (L - 1) означает размер заемных средств. Разность (R - Rf) означает, что для заемных средств мы уменьшаем доходность на процент по займу.

При этом стандартное отклонение (стд) такого портфеля с рычагом будет: SL = S * L. Т.е. прямо пропорционально размеру рычага. Буду считать это очевидным.

Дальше если выразить L = SL / S и подставить в уравнение RL, то получится как раз уравнение прямой CML, которое дано как определение в википедии. Печатать этот вывод формул лень. Я на бумажке проделал.

Справедливости ради надо сказать, что все это написано в статье в википедии. Только подается невзрачно. Без питча.

Вот релевантная цитата:

Область слева и над CML находится вне области допустимых значений, а нахождение справа и снизу от CML допустимо, но неэффективно.

Интересно, что я допер до этого почти сам. Я начал вдумчиво смотреть на кривую фронта в статье на сайте innoquantivity и заметил, что вместо QQQ можно взять точку с риском в два раза меньше и доходностью ниже всего лишь на три процента. Тут мне пришла в голову мысль посчитать доходность менее рискованого портфеля при условии, что я возьму рычаг 1:2. И да, даже при условии, что я буду занимать деньги под грабительские 7% в интерактив брокерс, доходность такого портфеля будет выше на 3%. Дальше начал мучить чат жпт, открыл ли я америку и да, таки открыл. Опаздал на 50 лет. Нобелевку не дадут.

Stan's ratio

Я придумал поменять коэфициент Шарпа, чтобы он стал более понятным для нубов.

Формула коэфициента Шарпа:

S = E(R - Rf) / Std(R - Rf)

Тут E(R - Rf) - это средняя доходность минус безрисковая доходность. Std - стандартное отклонение.

Предлагаю сделать два изменения:

1) перестать вычитать ставку рефинансирования;

2) домножить на стандартное отклонение sp500.

Тогда полученное значение будет проще интерпретировать. Это будет доходность инструмента отнормированная на средний рыночный риск. Его легко можно будет интерпретировать просто сравнивая с доходностью индекса sp500, т.к. риски будут выравнены нормировкой.

С коэфициентом Шарпа у меня проблема в том, что я вот смотрю на его значение и не понимаю это хорошее значение или нет. Надо сравнивать с чем-то. Можно сравнивать с значением показателя Шарпа для sp500. Но его еще надо найти, а лучше запомнить. А еще лучше сравнить значение с несколькими другими активами. В моем же коэфициенте ничего запоминать не надо. Сразу понятно о чем он говорит.

Наверняка я опять “открыл Америку”, но пока мне не известно кто это придумал до меня, поэтому буду называть это значение “коэфициент Стена”. Хотя это и не коэфициент вовсе. Но да ладно.

Stan's Alpha

В теории портфеля Марковица есть альфа и бета.

Альфа - это типа прибыльность бумаги за вычетом прибыльности рынка.

Бета - волатильность.

Раньше я бы читал википедию, но нынче разленился, спрашиваю чат жпт:

Альфа отражает эффективность управления активами по сравнению с определенным бенчмарком или рыночным индексом.
...
Бета измеряет волатильность или систематический риск инвестиционного актива по отношению к общему рынку или выбранному бенчмарку.

Мне попадались такие утверждения как “ищи альфу”. Типа надо гоняться не за прибыльностью, а за прибыльностью за вычитом волатильности.

Формула для альфы: a = Ri’ - b * Rm’. a - альфа b - бета Ri’ - доходность инструмента скорректированная на безрисковую доходность. Rm’ - доходность рынка скорректированная на безрисковую доходность.

Коррекцию на безрисковую доходность можно опустить. Она означает, что из доходности надо вычесть безрисковую доходность (процентную ставку по облигациям США).

Можно немного иначе смотреть на эту же формулу, если перенести Ri влево:

Ri = a + b * Rm

В таком виде та же самая формула воспринимается как линейная регрессия между доходностью инструмента и доходностью рынка.

Линейная регрессия - это когда есть облако точек и через н проводят линию. Облаком точек в данном случае являются доходности в разные моменты времени. По горизонтальной оси - доходность рынка, по вертикальной оси - доходность инструмента. Если есть корреляция, а она обычно есть, то точки начнут ложиться на некую линию. Тогда бета будет наклоном этой линии. Если бета больше единицы, то линия более крутая. Если меньше единицы, то менее крутая. Если меньше нуля, то вообще завалена налево. Альфа соответственно будет местом пересечения вертикальной оси в нуле.

(Мне тут пришла в голову идея, что можно было бы добавить еще и третье измерение - время и посмотреть как распределение точек будет меняться во времени. Было бы круто. Надо сделать.)

Вроде бы все понятно, но у меня все еще оставалось чувство отсутствия ясности. Поэтому я начал мусолить эту тему дальше.

Посмотрим на формулу для беты:

b = Cov(Ri, Rm) / Var(Rm).

Бета равна ковариации между доходностью инструмента и доходностью рынка, поделить на вариацию рынка. Вариация = дисперсия. Или же стандартное отклонение в квадрате.

Однако, это все для меня не очень понятно.

Ковариация характеризует насколько инструмент следуюет за рынком. Это понятно, но математически это неотнормированный коэфициент. Не понятно какие там будут значения и как их интерпретировать. Вариацию я к сожалению тоже не понимаю. Может кто-то понимает, но я увы нет. Мне проще понимать стандартное отклонение, т.к. это ширина распределения.

Так вот бинго и аха случилось когда я догадался правую часть формулы для беты домножить и поделить на стандартное отклонение доходности инструмента. Тогда вуаля и получается, что бета равна произведению коэфициента Пирсона на отношение стандартных отклонений инструмента и рынка:

b = p * std(Ri) / std(Rm),

здесь p - это коэфициент Пирсона, который принимает значения от минус единицы до единицы и характеризует насколько цена инструмента идет за рынком. А отношение стандартных отклонений тоже очевидно что такое.

Интересно, что я не нахожу какого-то устоявшегося названия для отношения стандартных отклонений инструмента и рынка. Поэтому буду пока называть это отношением Стена. И буду обозначать буквой s:

b = p * s

тогда формула для афльы:

a = Ri’ - p * s * Rm’

Сразу становится яснее значение альфы. Она равна доходности “дебафнутой” на доходность рынка помноженную на коэфициент корреляции Пирсона и на отношении стандартных отклонений.

Но все станет еще яснее, если поделить обе части равества на отношение Стена:

a / s = Ri’ / s - p * Rm’

величину a / s я предлагаю конечно назвать по традиции альфой Стена. Альфа Стен. Звучит.

Но если шутки в сторону, то на мой взгляд такая форма записи заметно понятнее.

Ri’/s - это доходность инструмента отнормированная таким образом, чтобы стандартное отклонение доходности этого отнормированного инструмента стало равно стандартному отклонению рынка. Т.е. мы сравняли их волатильности. Теперь эту доходность можно напрямую сравнивать с Rm’.

Дальше из этой отнормированной доходности мы вычитаем доходность рынка помноженную на коэфициент пирсона, который принимает значения от минус одного до одного. Тут тоже становится понятно, что мы делаем. Мы учитваем насколько следуюет инструмент за рынком.

Альфа Стена получается показывает насколько доходность инструмента выше доходности рынка. Тут можно сказать, что “здарсти, приехали. Это ведь и есть определение альфы”. Но есть нюанс, что моя альфа отнормирована таким образом, чтобы ее можно было напрямую сравнивать с доходностью рынка. Т.е. она отскейлена таким образом, что если мы получили +1%, то это не херпойми какой процент, а это ровно тот же процент, в которых расчитывается доходность рынка. Т.е. это процент доходности некоего синтетического инструмента, котоый отскейлен так, что его волатильность равна среднерыночной. Поэтому можно эту величину сравнивать с доходностью рынка напрямую. Елси получили +1%, то это прямо +1% к доходности рынка, а не +1%, который надо еще поправить, чтобы учесть волатильность.

Logitech Hero G502

Она просто офигенна. Не пожалел, что взял. Оказалось, что у нее еще в комплекте и грузики есть, чтобы сделать ее потяжелее.

Но главное конечно - это колесико. Оно такое какое должно быть. Если крутишь потихоньку, то можно без проблем прокрутить на один шаг. А если крутнуть как следует, то оно фигачит с инерцией.

Средний палец можно спокойно положить на колесико и не бояться, что заденешь другие кнопки, т.к. нет продолжения ЛКП и ПКП за колесиком, как бывает у некоторых.

Единственное, что лишнее для меня - это две кнопки слева от ЛКП. Но они не мешают.

Еще порадовало, что она запоминает свои настройки в отличие от A4tech, у которой после каждого включения компа приходилось три раза нажимать на кнопку регулировки точности.

Virtual monitors on popos

У меня была жутка ебля в прошлые выходные с тем, чтобы сделать виртуальные мониторы на лаптопе с PopOS.

В итоге все решилось и я даже отписался об этом в дискорде immersed. Продублирую тут, чтобы потом самому проще было найти:

I got virtual monitors on PopOS on a System76 laptop with Intel. But the steps described in https://medium.com/@augustoicaro/5b24bf1c4421 for intel didn't work for me. If I select "intel" driver in 20-intel.conf, then in syslog I see the error that /usr/lib/x86_64-linux-gnu/dri/i965_dri.so  is missing and a few lines later it says "Failed to submit rendering commands (Invalid argument), disabling acceleration." As a result I can create virtual monitors but the performance is horrible and also artifacts appear on the screen quite often. Maybe I had to install some drivers. But I'm not sure if it's a good idea to interfere with what system76 is doing. As far as I understand they manage driver updates automatically, though maybe I'm wrong. 
If I replace "intel" driver with "modesetting" (I actually don't know what I'm doing but just tried) then I get "modeset(0): Option "VirtualHeads" is not used" in the logs and the virtual monitor is not created.
I also tried to follow the steps for evdi approach but had issues there too. When I did "sudo modprobe evdi initial_device_count=4" my system got unresponsive. Mouse cursor was moving but all GUI was freezed. I had to press Ctrl+Alt+F3 and restart gdm with "sudo systemctl restart gdm". In logs I found "MESA-LOADER: failed to open evdi: /usr/lib/dri/evdi_dri.so". Finally I got it working after I installed displaylink-driver following steps on this page: https://www.synaptics.com/products/displaylink-graphics/downloads/ubuntu Again I don't know what I was doing but it helped. One thing I want to note is that I'm not sure that building evdi from the main branch is a good idea. Usually it's better to use a stable branch. Though I tried to checkout tags/v1.14.1 and it didn't helped in my case.

Кстати, после этого мне эти виртуальные мониторы пригодились еще раз, чтобы использовать старый лаптоп как второй монитор через https://deskreen.com/

После подключения патч кордом по LAN стало более менее. А по вайфай было совсем фигово с латенси. Хотя может это было от того, что старый лаптоп не может по 5G вайфаю работать.